Columna de Ciencia y Tecnología

Cristina Masoller

10.04.2017

Los sistemas complejos están constituidos por un gran número de elementos dinámicos que interactúan entre sí en forma no lineal, y cuya interacción da lugar a fenómenos emergentes globales que no se pueden comprender analizando el comportamiento individual de los distintos elementos del sistema.

Los sistemas complejos se estudian mediante las denominadas "redes complejas", en las que los "nodos" de la red representan los distintos elementos del sistema, y los enlaces o "links" representan las interacciones.

Ejemplos de sistemas complejos son las redes sociales (en Facebook, por ejemplo, las personas son los nodos y las relaciones de amistad son los links que las conectan), los sistemas ecológicos (las diversas especies son los nodos y las interacciones entre ellas se representan mediante links), las redes de energía (las estaciones de generación de energía y los consumidores son nodos de distinto tipo que están conectados mediante cables de distribución de energía que son los links), las redes de tráfico aéreo (los nodos son los aeropuertos y diversas las aerolíneas que los conectan son los links), las redes genéticas (los genes son los nodos y las interacciones entre ellos son los links), las redes de internet (las páginas webs son nodos que están interconectados mediante links), redes cerebrales (distintas áreas del cerebro constituyen los nodos que están interconectados ya sea físicamente, o bien funcionalmente -en este caso las conexiones representan áreas que se activan simultáneamente cuando se realiza una determinada actividad cognitiva, motora, etc.), redes climáticas (donde distintas áreas geográficas representan nodos que están interconectados mediante links que representan correlaciones en variaciones climáticas) etc.

Las redes complejas se caracterizan por tener una estructura organizada: no son completamente aleatorias, pero tampoco son regulares. Las redes complejas reales suelen estar organizadas en grupos de nodos altamente conectados (denominados "comunidades"), suelen también tener estructuras jerárquicas (tipo árboles o estrellas), y suelen estar constituidas por varios niveles ("multi-layer", por ejemplo, en las redes sociales, las conexiones en Twitter y Facebook representan distintos niveles de conexiones del mismo individuo).

La teoría de redes complejas, y más en general, la ciencia de la complejidad, es una de las áreas de investigación más activas de la ciencia moderna ya que incluye múltiples aplicaciones interdisciplinarias (en ingeniería, biofísica, neurociencia, etc.).

Determinar la estructura de la red a partir de datos observacionales es uno de los desafíos de la ciencia de la complejidad. Un ejemplo concreto se encuentra en las redes climáticas. En los últimos años, Marcelo Barreiro (profesor de la Facultad de Ciencias) y quien escribe (que desde hace años es profesora de la Universidad Politécnica de Cataluña, pero anteriormente fue también profesora de la Facultad de Ciencias) hemos colaborado en el marco de un proyecto europeo (LINC, climatelinc.eu) para utilizar la teoría de redes complejas para mejorar la comprensión de fenómenos climáticos. El clima es un sistema dinámico complejo por excelencia, compuesto por muchos subsistemas que interactúan entre si en distintas escalas espaciales y temporales. Utilizando el método de redes complejas, hemos colaborado en varios trabajos científicos donde se han estudiado la direccionalidad y las relaciones de causalidad de las variaciones de temperatura en las distintas regiones del planeta (conexiones de largo alcance, denominadas tele-conexiones climáticas), utilizando medidas de teoría de información para cuantificar las interacciones climáticas a partir de datos observacionales.

Varios investigadores uruguayos están trabajando activamente en teoría de redes, por ejemplo, recientemente un investigador del Instituto de Física de la Facultad de Ciencias, Dr. Nicolas Rubido, en colaboración con científicos brasileros, propusieron un nuevo método para identificar las comunidades de nodos altamente interconectados de una red compleja.

Para avanzar en la comprensión del funcionamiento y de la estructura de las redes complejas, es necesario desarrollar herramientas de análisis adecuadas que permitan comparar y distinguir con precisión la estructura de redes que cuentan con cientos de miles de nodos interconectados entre sí.

Descifrar estructuras, establecer diferencias entre conexiones y diagnosticar disfunciones es muy difícil. Actualmente, los métodos de análisis precisos son computacionalmente muy costosos y por tanto no se pueden utilizar en redes de gran tamaño. Los métodos de comparación de redes de gran tamaño se limitan a extraer sólo información parcial.

En particular, hasta ahora, no había una manera eficaz y precisa de reconocer la presencia o ausencia de enlaces críticos que conectan o desconectan la red, y por tanto, permiten o interrumpen el flujo de información.

En un trabajo reciente hemos propuesto una medida eficiente y precisa para la comparación de redes, que se basa en la cuantificación de las diferencias entre las distribuciones de probabilidad de distancia extraídas de las redes. Extensos experimentos en redes sintéticas y del mundo real muestran que esta medida permite identificar y cuantificar las diferencias topológicas estructurales que tienen un impacto práctico en el flujo de información a través de la red, así como la presencia o ausencia de enlaces críticos que conectan o desconectan la red.

Imaginemos por ejemplo que tenemos un sistema de distribución de energía compuesto por dos redes interconectadas con el mismo número de enlaces en cada una de ellas. A raíz de una avería, una de ellas pierde un enlace. Los métodos hasta ahora disponibles permiten sólo establecer la diferencia de enlace perdido. Nuestro método, además, tiene en cuenta la localización del  enlace perdido y su importancia en relación al sistema, es decir, si su ausencia dificulta significativamente la distribución de energía.

Gracias a esta nueva definición de distancia entre redes podemos generar redes sintéticas a partir de modelos matemáticos y analizar cuál es el modelo más cercano a la realidad. Esto permitirá determinar los mejores modelos para las redes que crecen por acercamiento geográfico, como las de transporte, o los mejores modelos para las redes que crecen por afinidad, como por ejemplo las redes sociales.

Esta investigación, que ha sido liderada por Martin G. Ravetti de la Universidad Federal de Minas Gerais (Belo Horizonte-Brasil) y de la que han participado Tiago A. Schieber (Universidad Federal de Minas Gerais), la autora de esta columna y Laura Carpi, del Departamento de Física de la Universidad Politécnica de Cataluña (UPC); Albert Díaz-Guilera, de la Universidad de Barcelona, y Panos M. Pardalos, de la Universidad de Florida (EE.UU), ha sido publicada en la revista Nature Communications.

http://www.nature.com/articles/ncomms13928

 

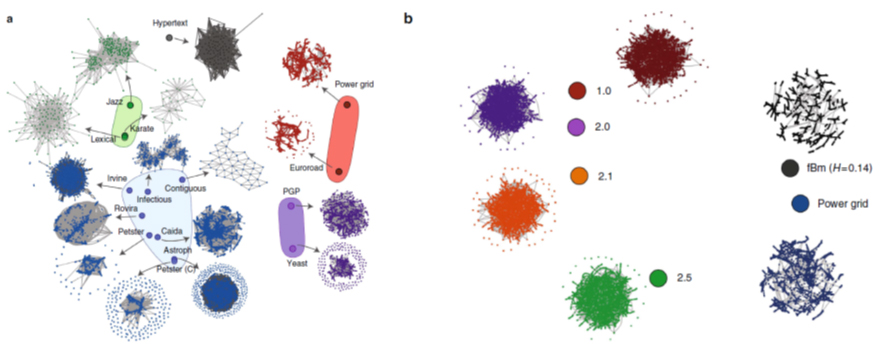
Figura: Representación esquemática de la distancia entre redes complejas de gran tamaño. En el panel (a) se comparan distintas redes entre sí (genéticas, sociales, de distribución de energía, etc.); en el panel (b) se compara la distancia de la red de distribución de energía con distintas redes sintéticas y se ve que la red generada con movimiento Browniano fractal es la más parecida. En otras palabras, el cálculo de la distancia permite encontrar el modelo de red sintética que es más cercano a la red real de distribución de energía.

Dra. Cristina Masoller (cristina.masoller@gmail.com)

Cristina Masoller obtuvo la Licenciatura en Física en la Facultad de Ciencias (UDELAR) en 1989, y la Maestría en el marco del PEDECIBA en 1991. Realizó sus estudios doctorales en Física en el Bryn Mawr College (BMC), Pennsylvania, Estados Unidos. Desde 2004 es docente en la Universidad Politécnica de Cataluña. Su área de investigación son los sistemas dinámicos no lineales, en particular, laseres, clima y modelos neuronales. Por más información, ver su página web http://www.fisica.edu.uy/~cris/

 

Por entregas anteriores de nuestra Columna de Ciencia y Tecnología, visite aquí.